A Tale of Tavern Mechanics

Patrons are people, too: An Order Algorithm

This post accompanies a major commit of Gnomebrew: The Tavern Mechanics, most crucially the mechanics of ordering drinks. Given the central role the tavern should play in the game throughout different stages of gameplay, giving this attention early is a good time investment.

Fair Warning: Comparated to others, this is a very technical post.

This post is a view into Gnomebrew's design and development process. While usually staying more high-concept, here we model functions. Some confidence in Math will be helpful in this write up.

Patron Personality

I would like my tavern simulation to be rooted in a bit of reality and some complexity and depth. So far, I have used very primitive flows to model the behavior of patrons. Now, I want to breathe some 'life' into patron decision making to increase variety and fun.

First and foremost, I want my patrons to have "personality". That word is often used, so I will define it for my purposes:

• From a gameplay perspective, I want patrons to act consistently across their lifetime (the patron that started a bar fight will probably not be seen calmly reading a book few minutes later). And, obviously, I want the behavior to be "fun" to play with.
• Coming from a background of education in a broader sense, I want the idea of patron personality be rooted in scientific consensus. Personality models like MBTI are still being used at large scale despite scientific evidence shrinking by the year. I don't want my patrons to be defined by a model proven by economic success, but rather scientific.

From that perspective, the only model that seems appropriate to me is the Big Five set of personality traits. They provide the most solid scientific backing to this date, which gives me some confidence of this model being a fitting base and additionally should yield a good amount of helpful research papers to base my modelling on.

Assuming each of the Big Five traits is normally distributed among my patrons and each trait is statistically independent from each other, I can model a patron personality quite simply:

@staticmethod
def generate_random_personality() -> dict:
    """
    Generates a dict (JSON) of a patron's personality
    :return:    A dict to be saved as the patron's personality.
    """
    personality = dict()
    personality['extraversion'] = random_normal(min=-1, max=1)
    personality['agreeableness'] = random_normal(min=-1, max=1)
    personality['openness'] = random_normal(min=-1, max=1)
    personality['conscientiousness'] = random_normal(min=-1, max=1)
    personality['neuroticism'] = random_normal(min=-1, max=1)
    return personality

Each personality trait's "intensity" is stored in a number value with -1 scoring incredibly low and 1 scoring incredibly high (>3 standard deviations respectively) on the trait. This makes modelling patron behavior convenient, as the (-1; 1)-range lends itself well to function modelling.

Now it's time to see how patron personality influences the game mechanics.

Patron Personality: Patience

Patience is relevant in a tavern, specifically when standing in queue to be served. When a patron decides to make an order, they enter the queue and wait for a specified amount of time. The wait time was before modeled as:

wait_time = timedelta(seconds=random_normal(min=120, max=user.get('attr.tavern.patron_patience', default=1200)))

An arbitrary time minimum (in this case 120 seconds, or 2 minutes) and an upgradeable attribute define the scope of waiting times across my patrons. The upgradeable attribute should definitely remain, as this is a reasonable dial to upgrade for the game experience I intend to create. I now want to make this modeling more interesting with the question being: How does the Big Five personality correlate with patience. Time for research!

A 2019 published paper by Iranian scientists is the first paper popping up in my research. It has spiritual overtones, focusing on a more volatile term 'Wisdom' which I don't consider helpful right now (however, if I ever get to design character stats, it's a starting point for the Wisdom component). Considering this paper comes from Iran where religious overtones are ubiquitous, I decide not to take to much concern with this right now. The paper is more concerned with the relationship of Big Five and Wisdom, using patience as an intermediate vehicle. It however provides correlation of three variables on patience.

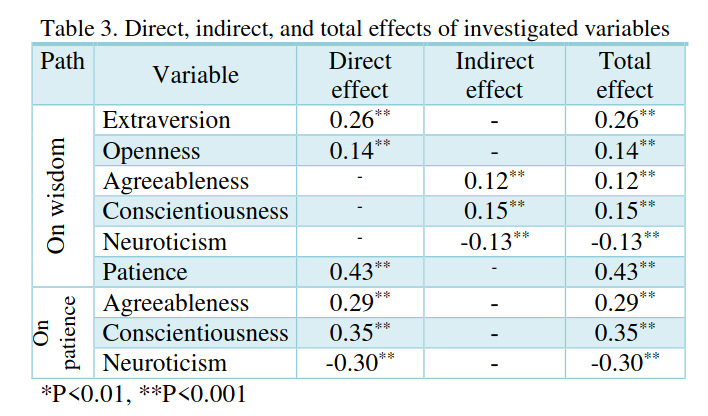
Finding more accessible literature seems difficult. The "mediating role of patience" seems to be a big deal in Iran, where more research papers on this are published (like this or this), unfortunately in Farsi, which I cannot speak. And of course, much more research that is potentially relevant to this is hidden behind dreaded paywalls.

Considering that I'm writing a game and not a thesis, I'll stop here and use the numbers from my starting paper. They can nicely be rationalized:

• Patrons scoring higher on agreeableness will likely be more patient, as they don't want to "rock the boat" and make a fuss about wait times.
• Patrons scoring higher on conscientiousness will likely be more patient, as they would tend less to "divert from the plan" and will likely have thought through the prospect of waiting in queue. They would not "spin on a dime" and leave soon if things take a little longer.
• Patrons scoring higher on neuroticism will likely be less patient, as they in tendency respond worse to stressors such as extended wait times.
• While no paper mentions a direct correlation with extraversion, I would assume that - to some extent - extroverted patrons will mind a long line to wait in less than introverted patrons.
• Openness to experience really should not make a signiicant difference here.

This brings me to this wait-time function:

def generate_wait_time(self, user: User) -> timedelta:
    # Base Willingness to wait
    wait_in_s = random_normal(min=1200, max=12000)
    # Calculate influence of personality on the patron as a factor
    personality_influence = (((self._data['personality']['agreeableness'] * 0.29) +
                                (self._data['personality']['conscientiousness'] * 0.35) +
                                (self._data['personality']['neuroticism'] * -0.30) +
                                ((self._data['personality']['extraversion'] - 1) * len(user.get('data.tavern.queue')) * 0.01)) *
                                user.get('attr.tavern.personality_flex', default=1)) + 1
    wait_in_s *= personality_influence
    return timedelta(seconds=wait_in_s)

This function is not perfect: personality_influence can technically get negative; a ridiculuously unagreeable, unconscientious, and neurotic person (-0.29 - 0.35 - 0.30 = -0.94) already is close to breaking the calculation, resulting in a 94% wait time reduction; and that does not take into account the additional wait time incurred through queue length (up to 2 additional percent points per person in line).

For now, I don't consider this a problem: This extreme scenario is highly unlikely, considering that it requires a patron to score three standard deviations away on multiple traits. Additionally, the worst case could be considered not a bug, but another feature: A patron so damn impatient that they leave the queue outright.

A more problematic element could be the calculation of extraversion-based waiting. This scales directly with the length of the tavern queue. At this point, I don't know yet how big this will grow (say at one point the player might serve a queue of > 20.000 patrons the formula breaks). For now, I'll keep it as is and get back to it as needed.

The attribute attr.tavern.personality_flex is a fun hookup for later. It allows dynamic adjustment of how intense personality influnences patron decisions. This allows for scenarios like a fey entering the tavern and excerting its' influence on everyone in the tavern and amplifying personal emotions.

Patron Personality: Gender & Names

So far, I have generated a random first name and a random last name out of lists of possible names. In the first name list, I had roughly equal distribution of male/female last names. To represent gender a little bit more vibrantly in gameplay, I am adding gender as a variable of each patron with options being male, female, and nonbinary.

Gender is randomly assigned during generation of the patron. Based on Williams Institute research, roughly 1.2M LGBTQ people identify as nonbinary in the US. Assuming a 328M population (based on US Census 2020), that's about 0.4% of the total population. I can use these numbers to inform human gender probabilities:

• 49.8% 'male'
• 49.8% 'female'
• 00.4% 'nonbinary'

Based on the patron's 'gender' stat, I can add more variance in gameplay for example:

• change potion effects
• inform patron romance probabilities
• adjust blood alcohol processing

Order Algorithm: Defining a patron's choice across gameplay

The order mechanic plays a very significant role in the simulation. Orders are the sole source of income in Gnomebrew across different stages of gameplay. Having a system that keeps these orders interesting, flexible, realistic, and balanced adds much value in moment-to-moment gameplay. It's definitely worth investing time into this.

So far, I used the most boring algorithm possible to define the order a patron makes:

• Either you order nothing
• Or you order one (1) beer

This was enough for basic testing, but now it's time for a more sophisticated system of generating a patron order.

A better order algorithm would:

• Take into account the personality of the patron.
• Take into account the environment (i.e. what's going on in the tavern).
• Return a variety of different order sizes (this is not as much relevant for realism but rather to have a sufficiently large "sink" for beer to get out of the game and turned into gold).

Order sizes are important for the game. The idea of an ever growing amoung of supply (higher and higher beer production) must be met with a similar increase in demand, otherwise the ingame 'economy' breaks and users do not properly benefit from the intended production growth.

Production can increase through:

• Higher amounts of raw materials available
• Faster production/recipe times
• Higher production capabilities (~more recipe slots)

To keep up with that, demand for the corresponding end products could increase through:

• More patrons in the bar (higher patron influx and higher patron capacity in bar)
• Larger orders per patron
• Higher budgets per patron

Supply and demand need to be somewhat 'balanced' throughout the entire game, as the game really centers around the production/selling dynamic. That however will be a challenge to tackle when the gameplay to balance around is implemented as well.

An Order Algo: Parameters

A nice algo needs to be found:

After a good amount of sketching as well as trial and error, I landed on a model I think is worth implementing:

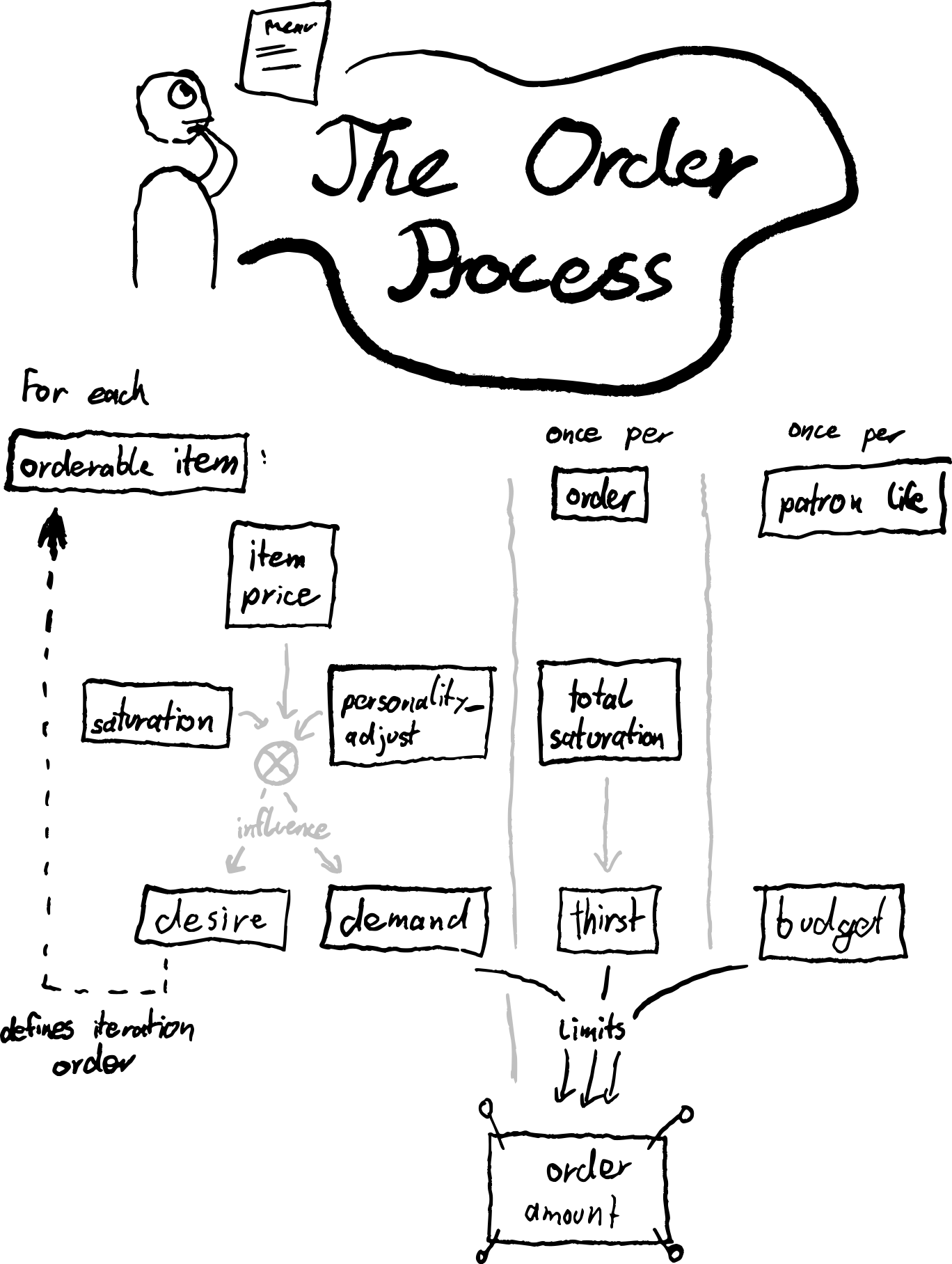
This flow contains several parameters that are used to make the multivariable decisions of an order. In the following paragraphs I'll introduce these parameters.

Saturation

Practically speaking, I need the order mechanics to 'soften out' during a patron's 'lifecycle'. This ensures that new patrons entering add more significant value to the gameplay rather than just being a number that changes in the interface.

The more a patron already pleased themselves with your fine drinks, the less satisfaction they will experience from the same amounts. Simply put: After 10 beers, the 11th is not quite as satisfying as your first one was. A nice way to model it is this:

• The first beer creates any level of satisfaction, let's standardize that as 1
• The second beer makes half of the total beer so far, it's 'mass' relative to the total beer so far is 1/2
• The third beer makes a third of the total beer so far, so 1/3

I recognize a Harmonic Series when I see it. That let's me approximate the cumulative value of any amount of beer as (in other words: saturation):

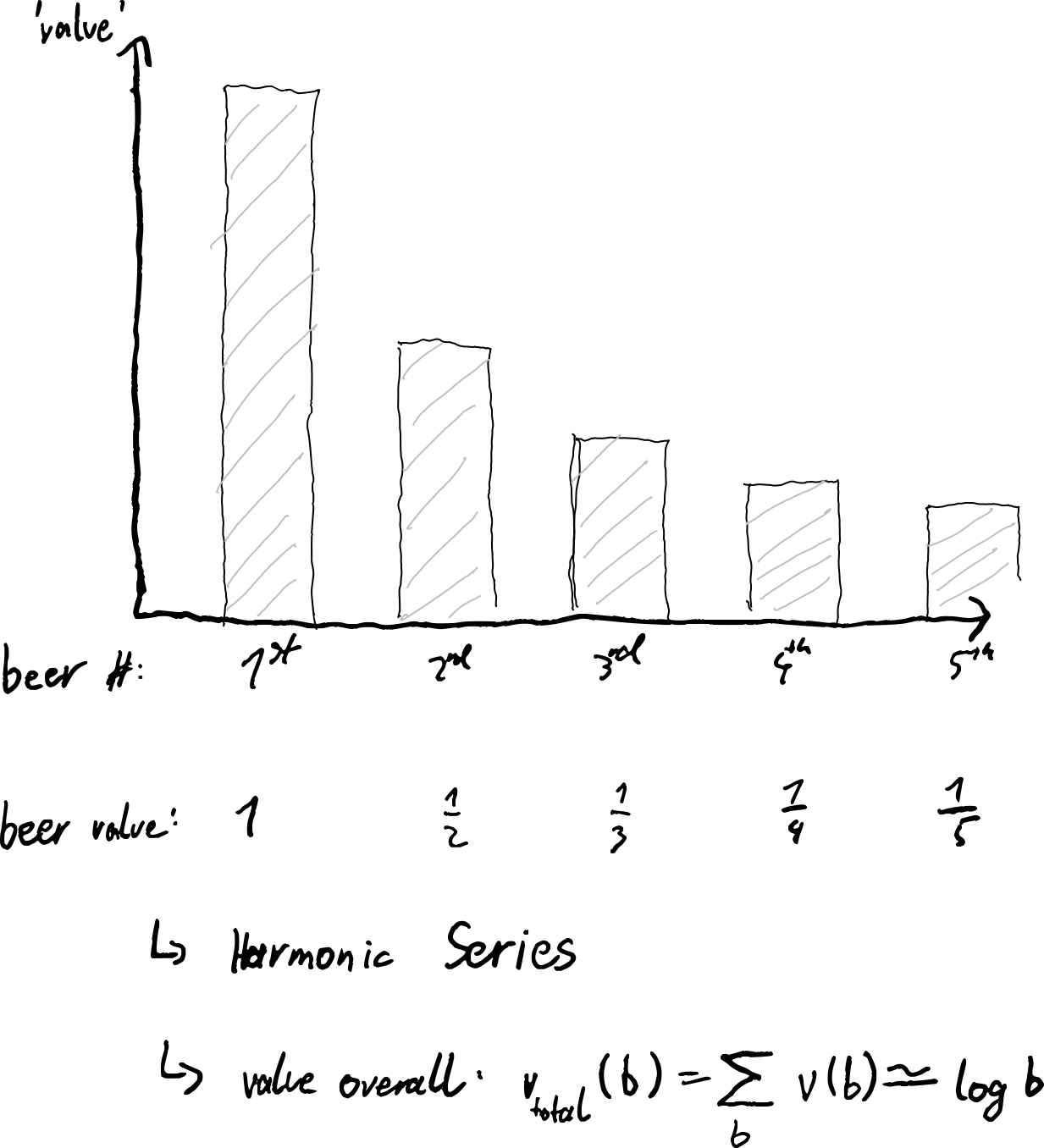
I abstract this to a saturation factor of ln ( c * b + e ) where b is the number of items of this type alread consumed and c is a dynamic dial parameter to balance the factor in upgrades and item-specific base values.

This formula ensures that:

• Saturation takes no effect at no items consumed (ln(c*0 + e) = ln(e) = 1).
• Saturation increases 'fast' and slows down with increased item consumption, only being recognizable when a new order of magnitude is reached. This makes this progression mechanic attractive for a type of game where orders of magnitude are being breached regularly.

I can have a Patron now calculate this:

def calculate_saturation_factor(self, orderable_item: Item, user: User) -> float:
    if orderable_item.get_minimized_id() in self._data['tab']:
        return log(self._data['tab'] * orderable_item.get_value('orderable')['saturation_speed'] * user.get(
            'attr.tavern.saturation_factor', default=1) + math.e)
    else:
        # Not ordered this yet. Factor = 1
        return 1

This factor is used to curb most of the key parameters in the order algorithm.

Personality Adjust

To account for patron personality, each orderable item correlates with personality-specific preferences: Each item can generate a personality_adjust percentage that reflects how much larger/smaller (in percent) the actual demand/desire/etc. should be based on personality. For this, each orderable item receives game data that specifies how much any personality aspect influences this parameter.

An excerpt from item.simple_beer JSON:

{
    game_id: 'item.simple_beer',
    orderable: {
        personality_adjust: {
            extraversion: 0.1,
            neuroticism: -0.05
        }
    },
    name: 'Beer',
    description: 'Well, it\'s beer.'
}

Each numeric value represents the max contribution to personality_adjust per variable. E.g. a half extraversion (0.5) and min neuroticism (-1) person would experience a personality_adjust of 0.5 * 0.1 + -1 * -0.05=0.1, so 10% to values like item-specific desire or demand.

The code is simple:

def demand_to_personality_adjust(self, personality: dict) -> float:
    adjust_val = 0
    for adjustment in self._data['orderable']['personality_adjust']:
        if adjustment in personality:
            adjust_val += self._data['orderable']['personality_adjust'][adjustment] * personality[adjustment]

    return adjust_val

Item Price

I'm making life easy for me here and focus on the actual price (as set by the player) vs. what the patron would consider a fair price. The latter value is defined by the game based on the item's base value and possible player upgrades.

Any item can define its' current fair price easily:

def determine_fair_price(self, user) -> float:
    return self._data['base_value'] * user.get('attr.tavern.price_acceptance', default=1)

Now the ratio current_price/fair_price is a quantity I can use to bring price into order decisions.

Demand

Demand simply limits the amount of items of this kind a patron is willing to order. The 'law' of Supply and Demand is the best option to base this on. Simplified:

• Higher prices = less demand = lower order amounts
• Lower prices = higher demand = higher order amounts

I am modeling this with a hyperbolic curve:

• A price close to 0 means patrons will buy a lot (however, everyone has limited thirst effectively capping off purchases), represented with the asymptotic rise to infinity.
• The higher the price, the lower the demand, approaching 0.
• At the 'fair' price there will be a 'fair demand' (modeled in the item data as constants). For the purposes of modeling this function, fair price and demand will be 'normalized' to 1.

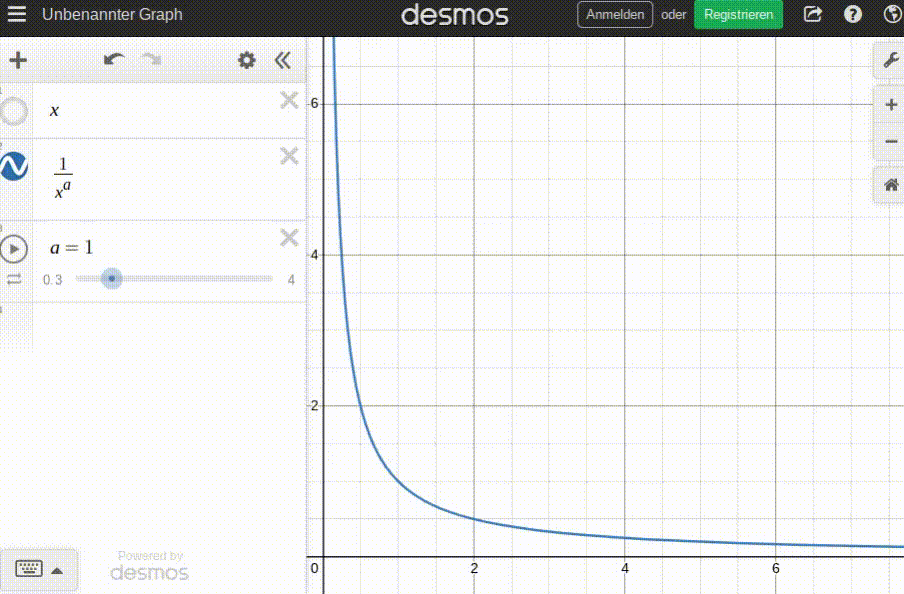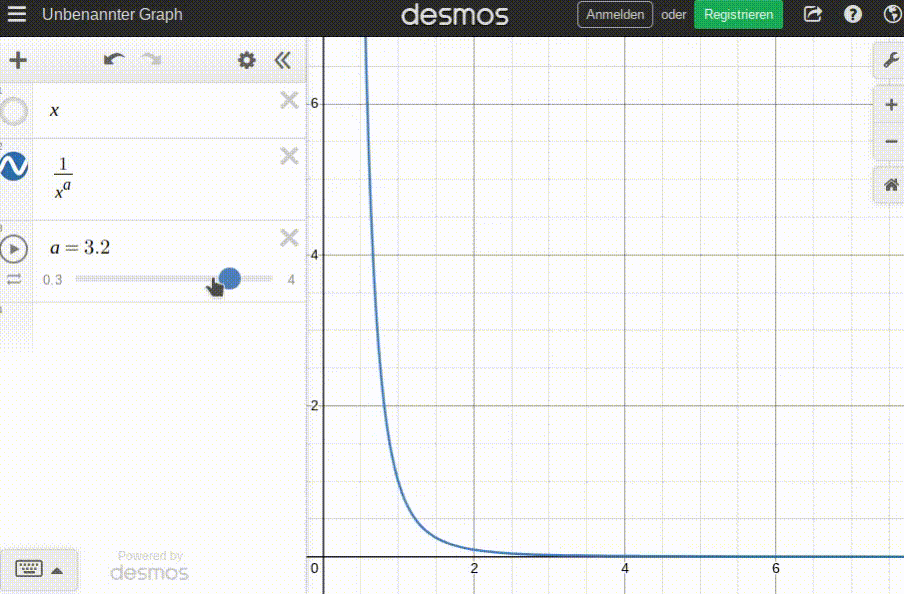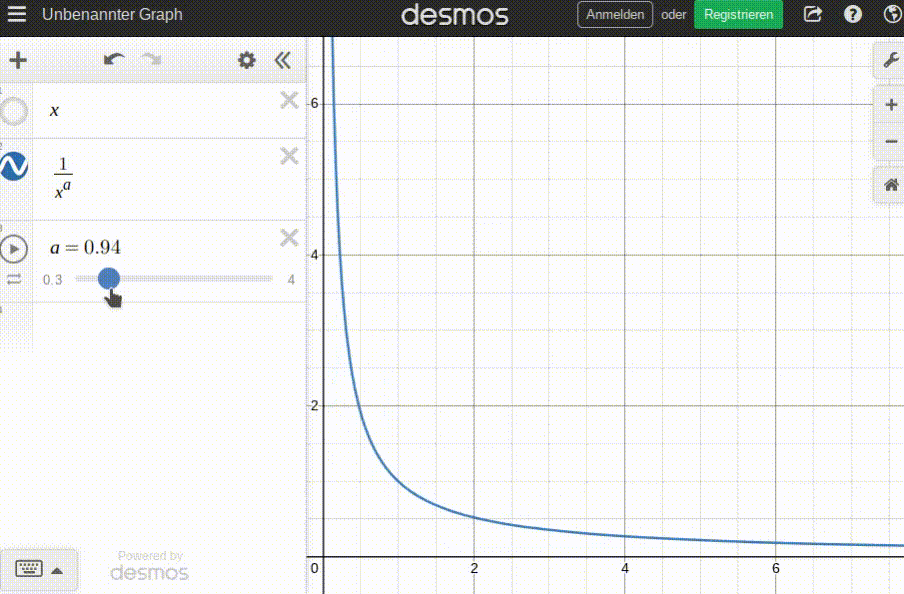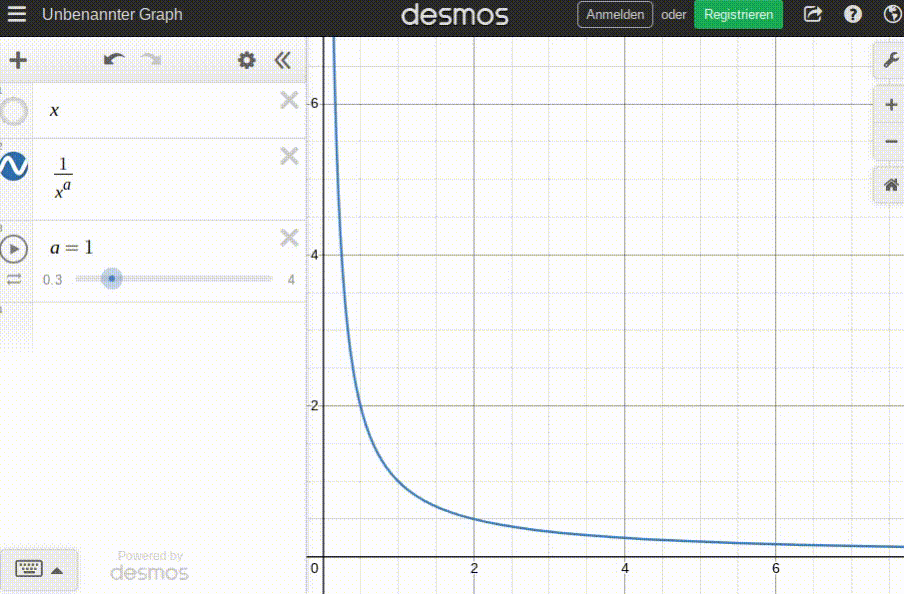
After much trial and error, and a learning things about hyperbolas I didn't know existed, I am modeling the basic demand function d as:

d(p) = 1/p^a

With:

• p being expressed as multiples of the fair price (p=1 ==> p=p_fair). This makes the modeling of functions much easier, as I can now assume that d(p_fair)=1 always is true.
• a being an item-specific factor of price elasticity and a>0. The higher a, the more elastic the price (i.e. the more demand 'reacts' to price changes).
• d(p) being expressed as multiples of a fair_demand value specific to the item. Therefore, d(p_fair)=fair_demand.

Now this curve needs to be curbed by saturation. Loosely spoken, saturation correlates inversely to demand: The more saturated the 'market', the lower the demand. So we divide by the already defined saturation factor:

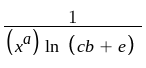
Some animation to get a feel for this function; this is how the price/demand curve changes with the number of items already consumed before ordering (b):

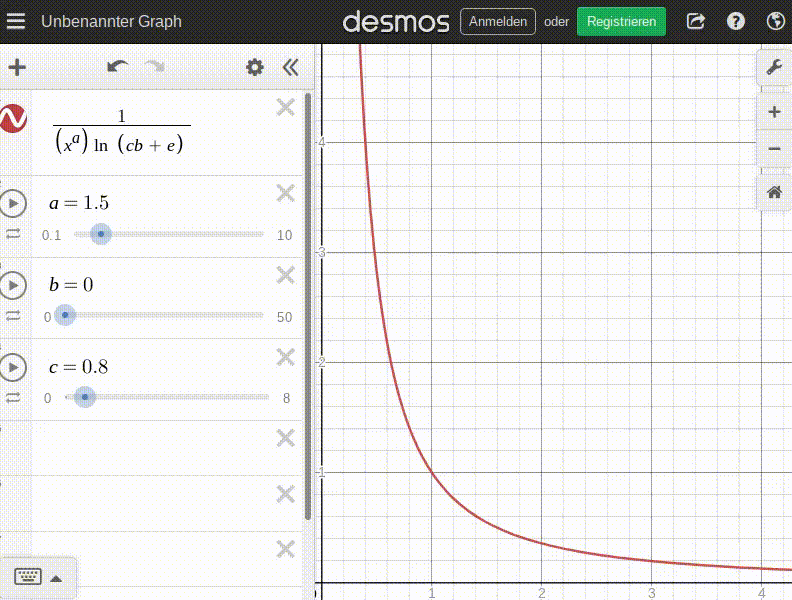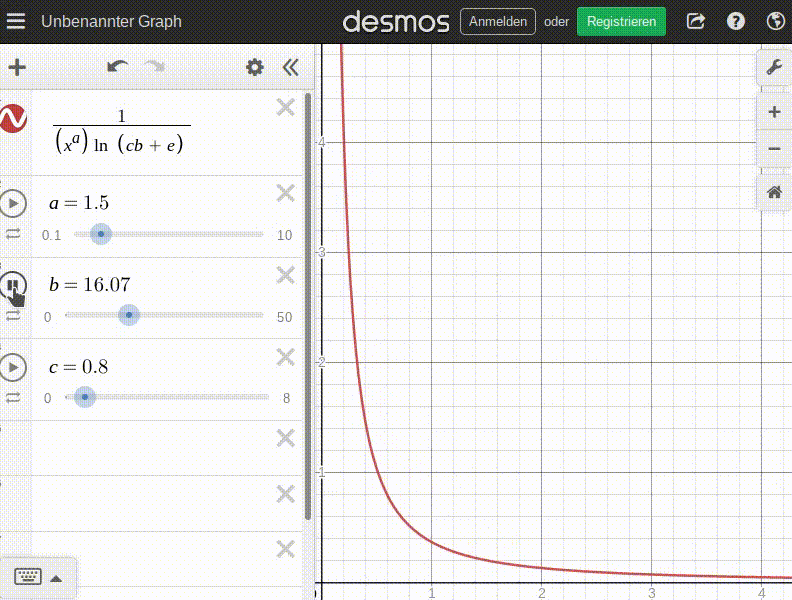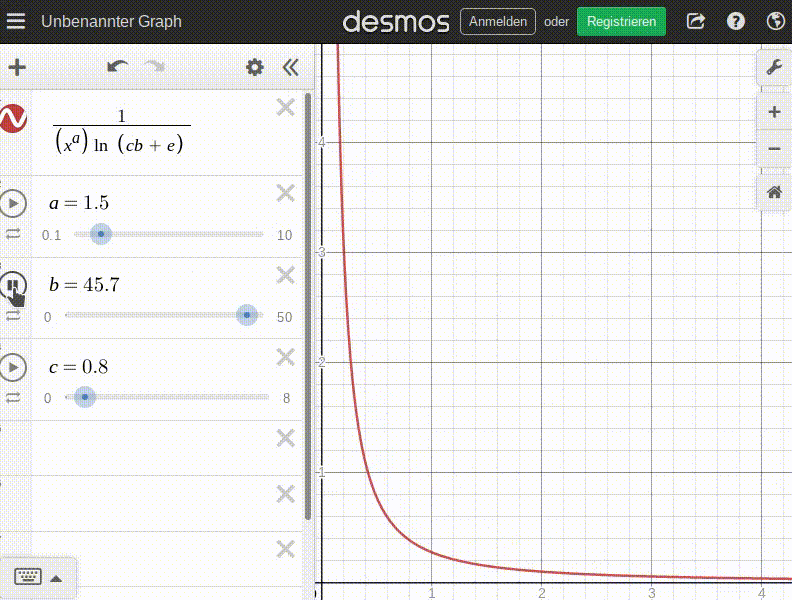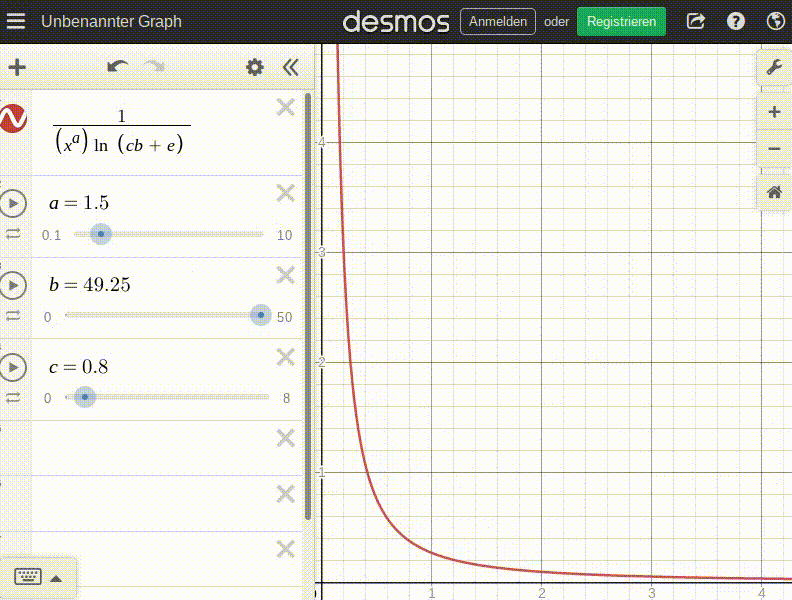
Additionally, I want the patron's personality to also factor in to this, so I'm factoring in personality_adjust.

This is enough calculation for demand, I think. (I'm curious and a little terrified of larger scale performance tests already...)

Only minor things I need to add now:

• Scaling by fair demand: Each item has a designated fair_demand that represents the expected demand at the fair price. Since we designed the function accordingly, this can simply be put in the numerator.
• Noise: This calculation is exact, and I would like some fuzziness still. In order to do that, I take the result and run it through a simple utility fuzzify, which applies some random deviation to the result.
• Round down: I want the demand to represent an exact number of how much the patron would like to buy (nonwithstanding factors like budget), so the overall result will be the floor of the final calculation.

With that, I can bring everything together in this monster (simplified):

def generate_demand_for(self, orderable_item: Item, current_price: float, user: User) -> int:
    orderable_data = orderable_item.get_value('orderable')
    personality_adjust = 1 + orderable_item.demand_to_personality_adjust(self._data['personality']) * user.get('attr.tavern.personality_flex', default=1)
    saturation_factor = self.calculate_saturation_factor(orderable_item, user)
    return floor(fuzzify(personality_adjust *
                            orderable_data['fair_demand']/((current_price/(orderable_item.get_value(
                            'base_value') * user.get('attr.tavern.price_acceptance',
                                                        default=1))) ** orderable_data['elasticity'] * saturation_factor)))

Desire

Demand reflects the relationship between price and order amount but does not create any relationship between different items to order. To create a metric to compare different purchase options, I am modeling a desire curve.

This is projected on the unit intervall [0;1] with 0 being undesired and 1 being incredibly desired. A patron will keep ordering items in descending order of desire until they are fully satisfied or they run out of money/thirst.

Let's get to it!

The relationship between price and desire is more intricate than the price-demand relationship:

• Things that are 'too cheap' can be perceived as of lesser value.
• Things that are incredibly expensive can be perceived as of greater value.

Therefore, I want the graph describing this relationship to be less straightforward:

Now I need to find an elegant curve to model this mathematically. A short eternity and lots of fiddling later I found a solution that looks good (at least when plotted). An animated gif says more than a thousand words:

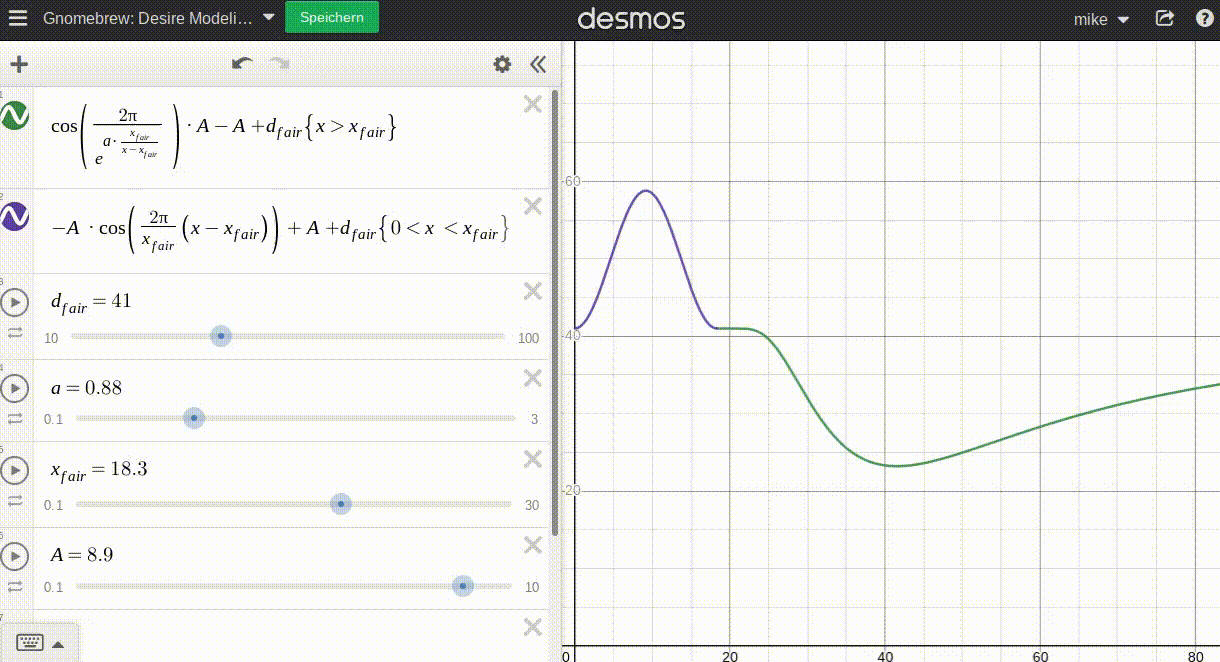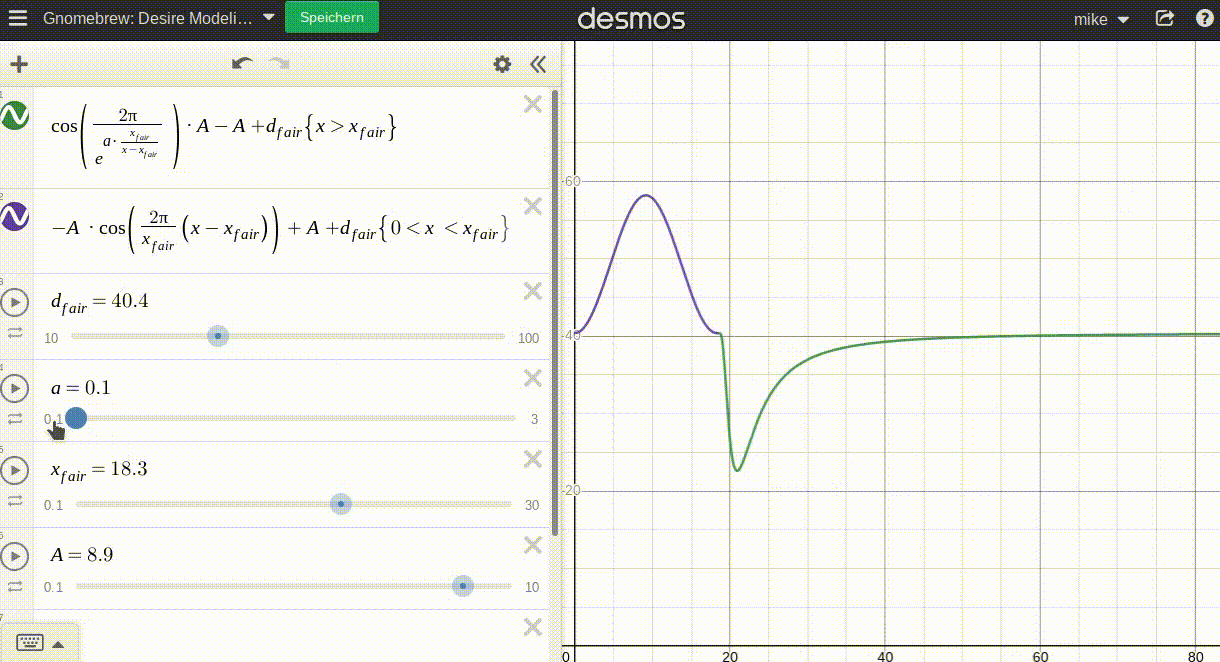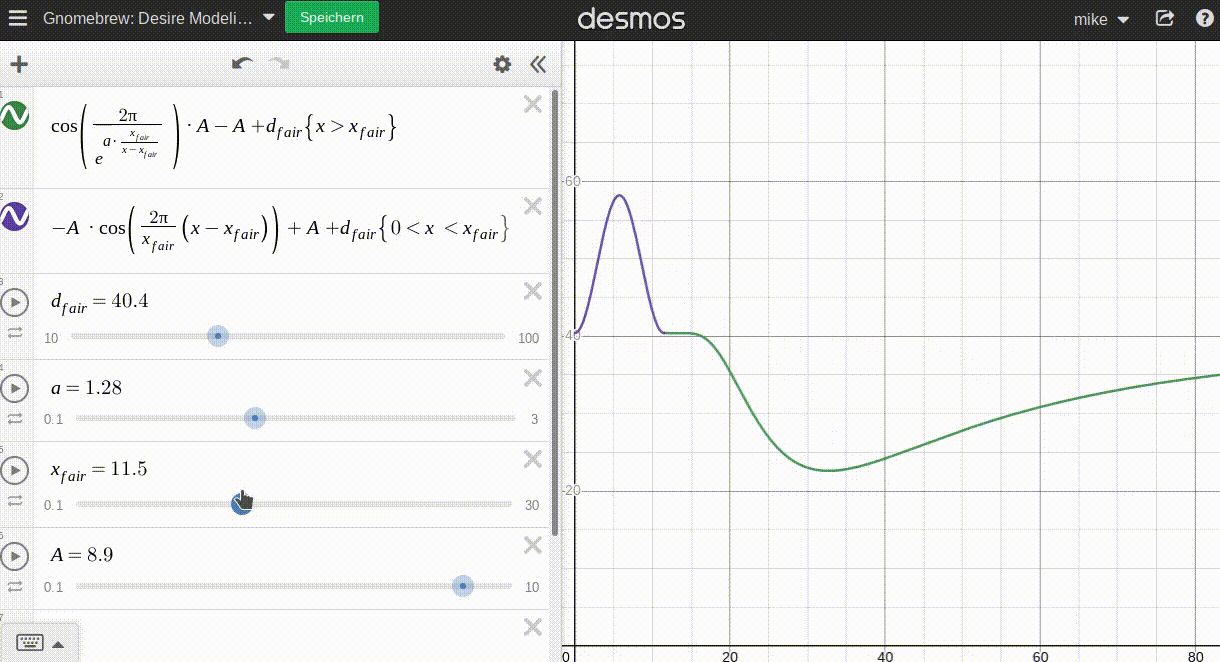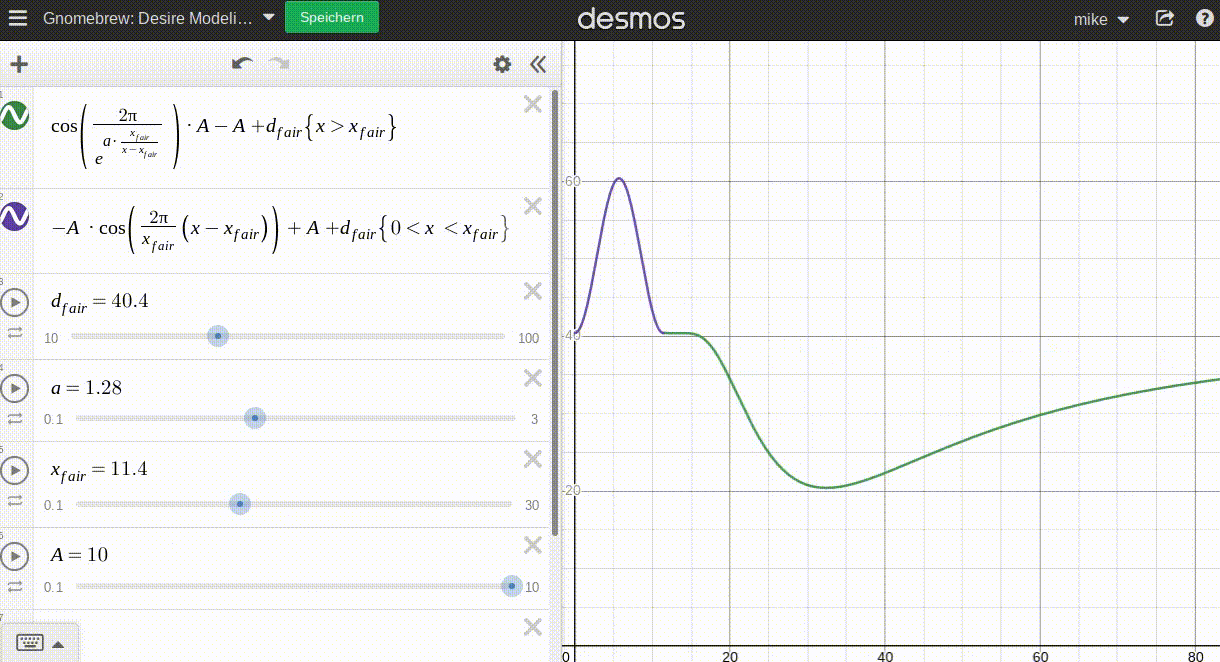
Where:

• d_fair represents the 'average' desire at the fair price x_fair
• a is a parameter that determines how fast the 'luxury effect' kicks in. The lower a, the faster the effect kicks in.
• A represents the 'amplitude' of this function, the difference between average desire and highest/lowest possible desire.

The graph is split in two separate functions at the fair price. Now using p instead of x, the concept is:

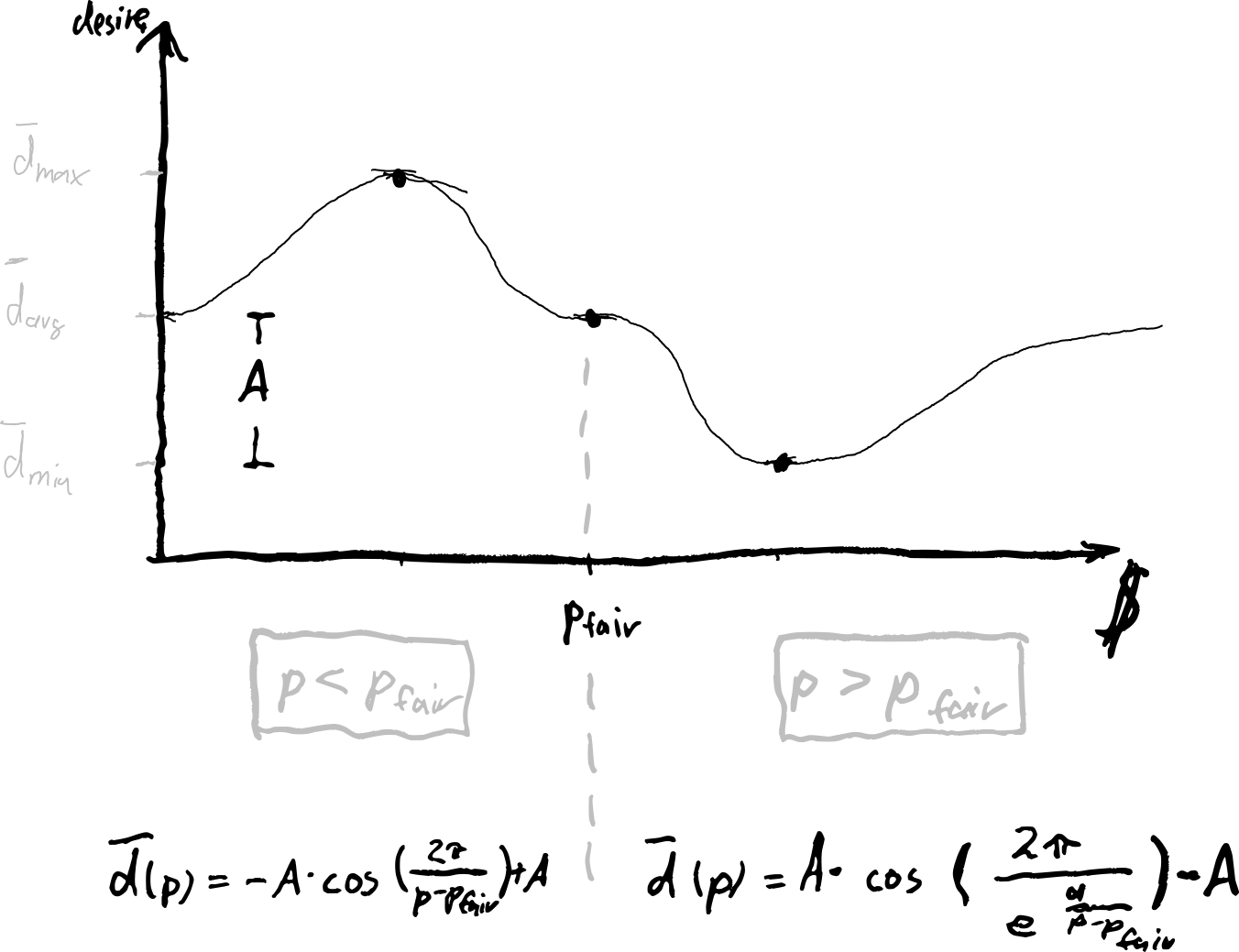
I use two cosine functions to model both sides around the fair price p_fair:

• The left side is a simple cosine period moved and adjusted accordingly.
• The right side is a modified cosine period asymptotically approaching its' period end with a parameter a to help adjust the rate at which the movement takes place; again, moved accordingly.

With desire(p_fair)=d_fair the function is continuous and even neatly differentiates at p_fair. Good enough for Gnomebrew!

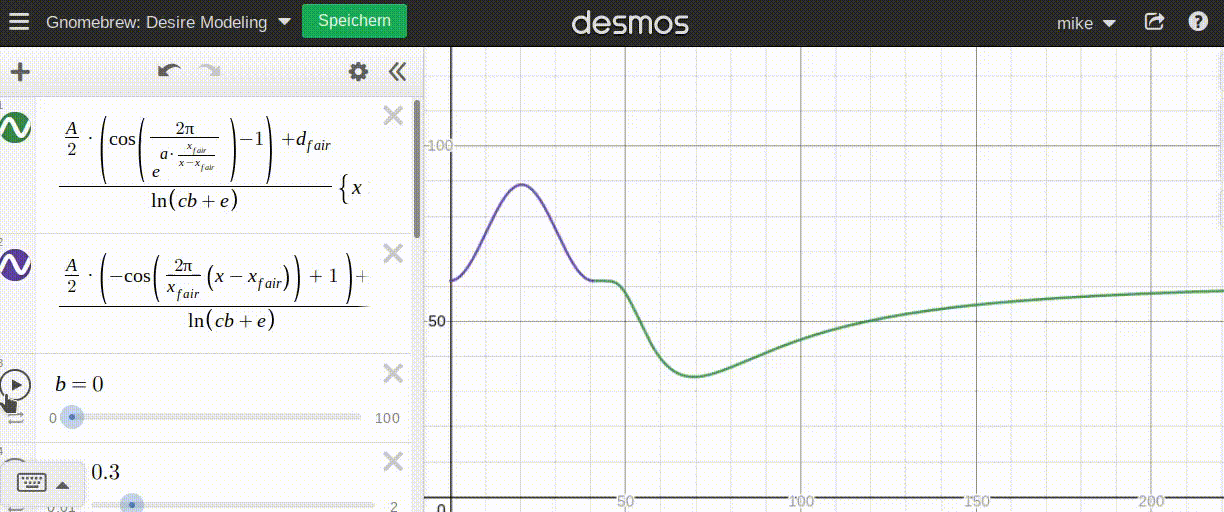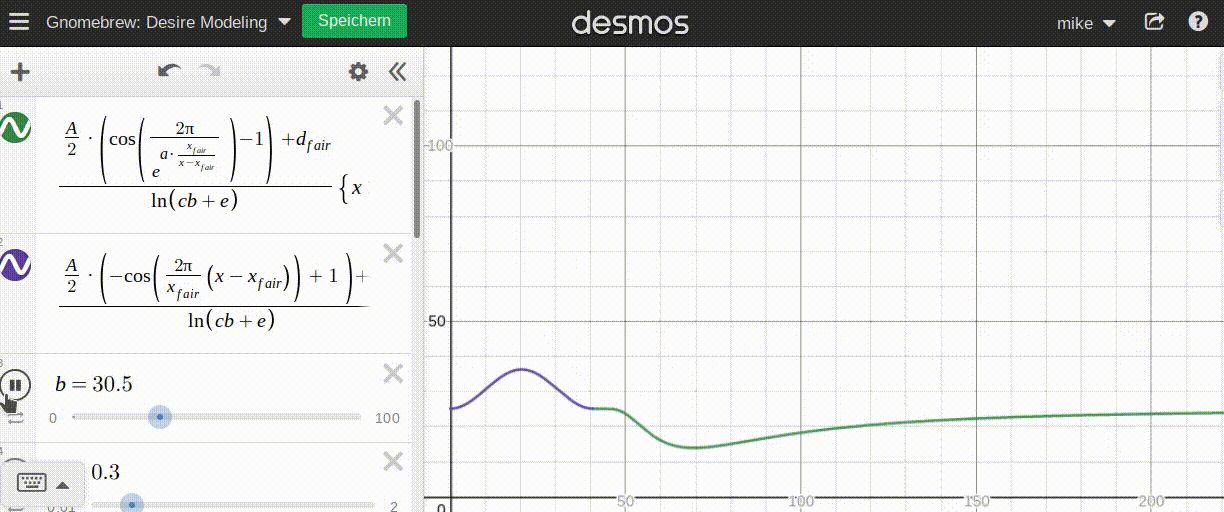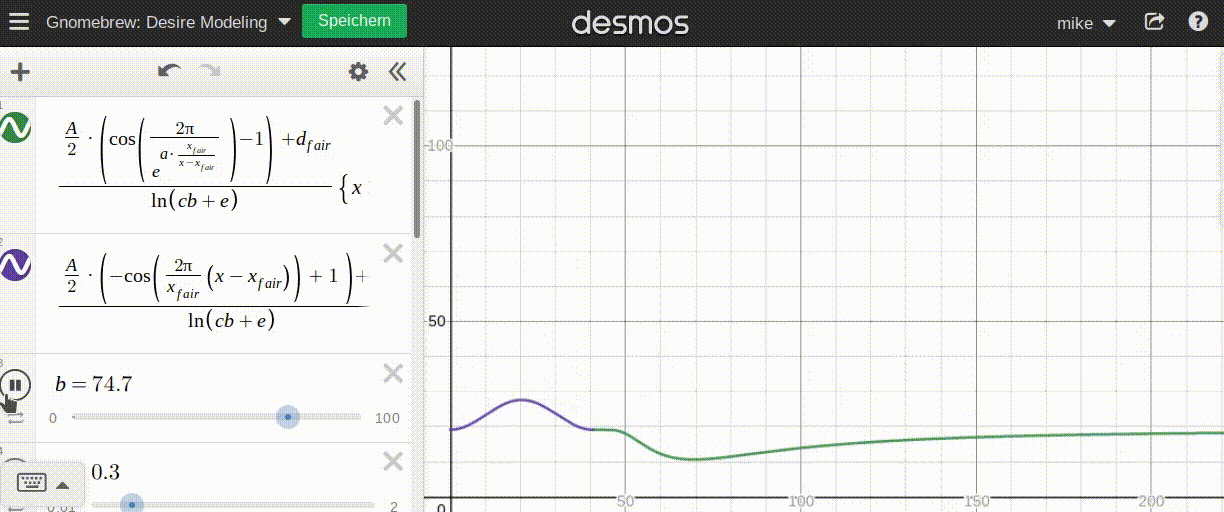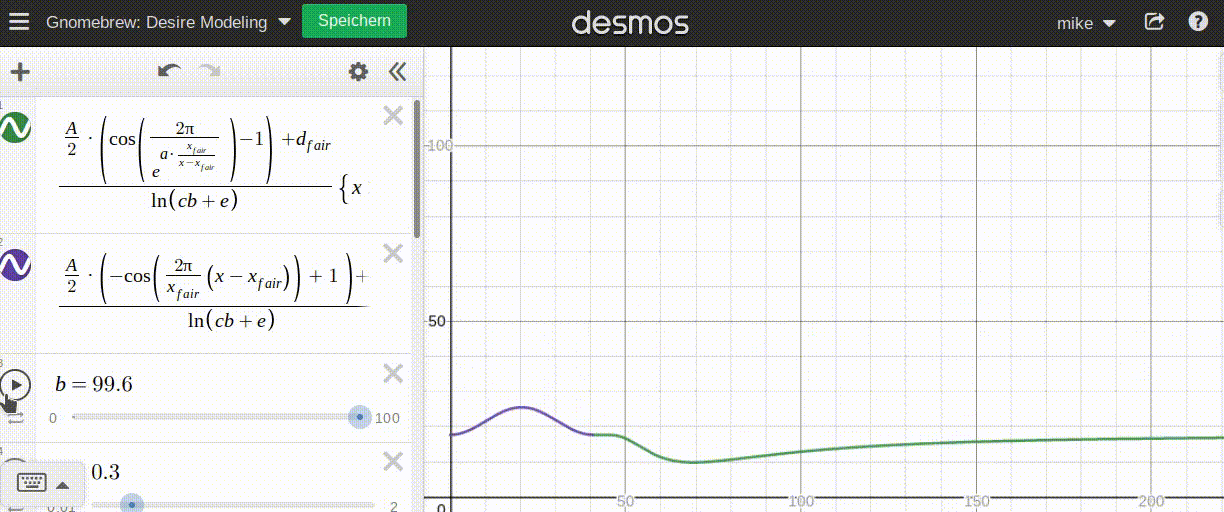
Similarly to demand, the more saturated the 'market' (or specifically the deciding patron) is, the less desire they have to get more. Since I have designed this aspect already, I will use the saturation factor exactly as I did for demand:

Unlike demand, which can go arbitrarily high (hypothetically, a patron could demand any number of drinks), desire is capped between 0 (no desire) to 1 (max desire).

This allows me to:

• Compare different items to order easily by desire, as that values stays in the defined and limited [0;1] region.
• Keep my focus separated between order quantities (demand) and item priorities (desire).

To do this, I am reducing some parameters by setting their values fixed: By setting d_fair=0.5 and A=0.5 the function is limited to the [0;1] channel. Exactly where I want it.

The moving parameter a can also be removed. I think its value is rather limited as it only pertains to the 'right' side of the curve. On the left side, the highest point is always at 0.5 * p_fair. Similarly, I want the lowest point of the desire curve to always be at 1.5 * p_fair.

To ensure this, I need to set a to ln(2)/2. If you like to check why, you can look at my napkin math for this. Nicely enough, this allows me to cut some corners: If I change the exponentiation base to sqrt(2), I can remove a entirely (more napkin math to further simplify. Assuming exponentiation runtime doesn't change significantly with chosen base (that's quite an if though), this should be an efficient solution.

Adding the saturation factor, this gives me these formulas for my desire function:

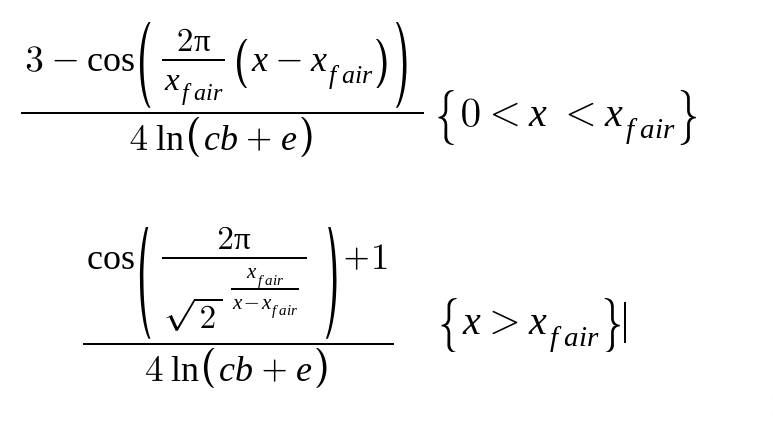
Lastly, the personality_adjust factor is applied. Since this could technically move the result out of [0;1], I cap the output at these borders, yielding the algorithm:

    def generate_desire_for(self, orderable_item: Item, current_price: float, user: User, **kwargs):
        saturation_factor = kwargs['saturation']
        fair_price = kwargs['fair_price']
        personality_adjust = kwargs['personality_adjust']
        if current_price < fair_price:
            denominator = 3 - math.cos(TWO_PI * (current_price - fair_price) / fair_price)
        elif current_price > fair_price:
            denominator = 1 + math.cos(TWO_PI / math.pow(ROOT_TWO, fair_price/(current_price-fair_price)))
        else:
            # Current price is fair price exactly ==> 2 (so that denominator/4 = 0.5)
            denominator = 2
        base_value = denominator/(4*saturation_factor)

        # Apply Personality shift
        return max(1, min(0, base_value*personality_adjust))

Thirst

Even the most wealthy patron will not buy more than they need/want. I abstract this as a patron's thirst, which in and of itself would not depend on supply/pricing. The patron's determined thirst defines the maximum amount of 'value' the patron would like to order in this cycle (each item to order has a defined thirst-quench/unit value to reduce thirst by consumption). Even if the bar prices are incredibly attractive (e.g. 0.0001 gold for some beer), patrons can't order more than dictated by their thirst (they can, however, come back more often on lower prices before their cash runs out).

A patron's thirst depends also on personality. A Spanish study nicely links some Big Five traits with alcoholism behaviors. The result section lists correlations I can make use of for the game:

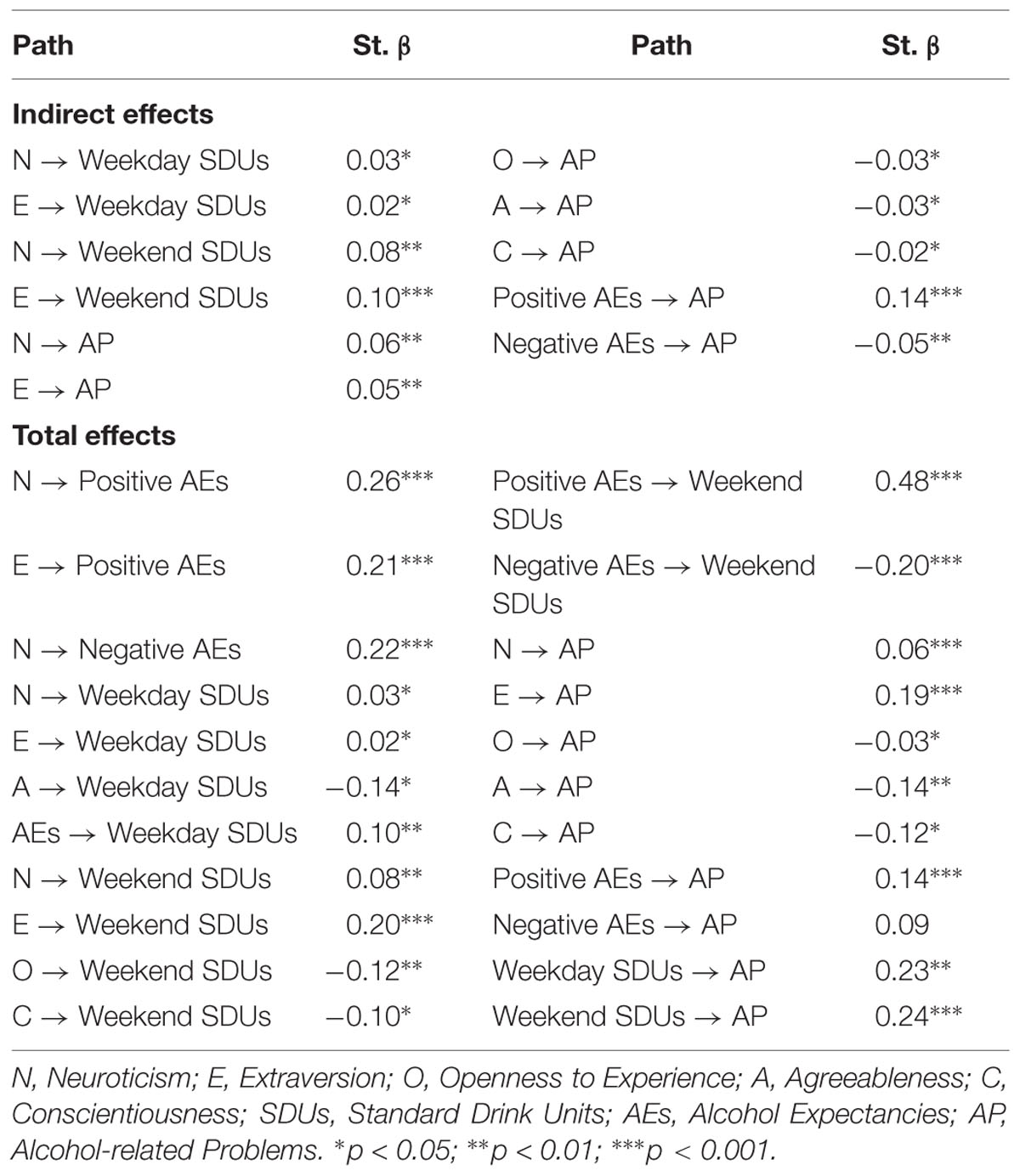
Most interesting to me here is the amount of beer patrons might purchase. Here, the SDUs (standard drinking units) are relevant. Since the numbers are organized in weekday vs. weekend, why not apply the same in Gnomebrew? Thanks to StackOverflow I can briefly code a is_weekday() utlity and apply different modifiers based on the actual day of the week in-game. The caveat here is the server time: Gnoembrew runs in UTC. If a user plays in a time zone far off (e.g. UTC+20), they will perceive the logic to run differently. For now, I will be OK with this. Considering I can easily patch a fix for that in (e.g. getting and using data from current_user), I will leave this be for the time being.

Other than personality, also the saturation influences thirst. After 20 drinks I'm less thirsty than before. I'm adding the same logarithmic saturation factor, just this time adding up the total amount of drinks rather than considering the individual saturation per item. To make sure I understand this well enough to balance, I must understand: How does using ALL drinks available influence thirst compared to individual saturation?

To understand how these different saturation factors correlate, I did more napkin math that shows: The total saturation differs from an individual saturation by ln(N) on average, where N is the amount of different items on the menu. This is great news: Since the number of items in the price list N will be limited, the difference between item-individual and total saturation will be rather small. Assuming similar constants c for all items, the difference between average individual and total saturation would grow only logarithmically: For 200 orderable items (which is a very ambitious number), the difference between total and individual saturation would be on average ln(200)= 5.3 units.

Therefore, I expect the thirst to approach it's current equilibrium faster than individual item saturation.

With everything together, I can define a thirst function:

def generate_thirst(self, user: User, **kwargs) -> float:
    if is_weekday():
        personality_influence = ((self._data['personality']['agreeableness'] * -.14) +
                                    (self._data['personality']['extraversion'] * .02) +
                                    (self._data['personality']['neuroticism'] * .02)
                                    * user.get('attr.tavern.personality_flex', default=1)) + 1
    else:
        personality_influence = ((self._data['personality']['neuroticism'] * .08) +
                                    (self._data['personality']['extraversion'] * .02) +
                                    (self._data['personality']['openness'] * -.12)
                                    (self._data['personality']['conscientiousness'] * -.10)
                                    * user.get('attr.tavern.personality_flex', default=1)) + 1

    saturation_factor = kwargs['saturation_factor']

    base_thirst = random_normal(min=MIN_BASE_THIRST, max=MAX_BASE_THIRST)
    return base_thirst * personality_influence * user.get('attr.tavern.thirst_multiplier', default=1) / saturation_factor

Writing an actual Order Algo

With all helping parameters defined and a complete model, I can now finally write the actual core algorithm to define a patron's decision on what/how much to order:

def decision_step(self, user: User):
    prices = user.get('data.tavern.prices')
    # I'm noting down my orders here
    order_list = []

    # I'm managing my order preferences here
    wish_list = []

    # Take a look at the menu. Assign a perceived value to each item and create a wish-list
    # sorted by my desire to buy
    for item in [Item.from_id(f'item.{it_id}') for it_id in prices]:
        saturation = self.calculate_individual_saturation_factor(item, user)
        fair_price = item.determine_fair_price(user)
        personality_adjust = 1 + item.personality_adjust(self._data['personality']) * user.get(
            'attr.tavern.personality_flex', default=1)
        current_price = prices[item.get_minimized_id()]
        wish_list.append({
            'desire': self.generate_desire_for(orderable_item=item,
                                                current_price=current_price,
                                                user=user,
                                                saturation=saturation,
                                                fair_price=fair_price,
                                                personality_adjust=personality_adjust),
            'demand': self.generate_demand_for(orderable_item=item,
                                                current_price=current_price,
                                                user=user,
                                                saturation=saturation,
                                                fair_price=fair_price,
                                                personality_adjust=personality_adjust),
            'item': item
        })
    wish_list = sorted(wish_list, key=lambda d: d['desire'])

    # I am motivated to order. Let's go:
    # Go through my wish list in descending order of preference and start ordering

    total_saturation = self.calculate_total_saturation_factor(user=user)
    thirst = self.generate_thirst(user, saturation_factor=total_saturation)
    budget_count = self._data['budget']
    desire_threshold = AVG_DESIRE_THRESHOLD * user.get('attr.tavern.desire_threshold_factor', default=1)

    for wish in wish_list:
        item_name = wish['item'].get_minimized_id()

        # Check if minimum requirements for all four parameters are met:
        if budget_count > prices[item_name] and \
                thirst > 0 and \
                wish['demand'] >= 1 and \
                wish['desire'] > desire_threshold:
            orderable_data = wish['item'].get_value('orderable')
            # I want the most possible of this limited by:
            # a) Budget
            # b) Thirst
            # c) Demand
            amount = int(min(floor(budget_count / prices[item_name]),
                                ceil(thirst / orderable_data['thirst_reduction']),
                                wish['demand']))
            budget_count -= amount * prices[item_name]
            thirst -= amount * (
                    orderable_data['thirst_reduction'] * user.get('attr.tavern.thirst_reduction_mul',
                                                                    default=1))
            order_list.append({
                'item': item_name,
                'amount': amount
            })

    if not order_list:
        # My order list is empty. I can't afford/don't want anything. Let's leave.
        self.leave_tavern(user)
        return

    # I have finished my order list. Time to enqueue!
    self.enter_queue(user, {
        'id': self._data['id'],
        'order': order_list
    })

The algorithm steps:

1. Calculate desire & demand for all items
2. Calculate total thirst
3. For all items, in descending order of desire:
   1. Make sure minimum requirements for price (can I afford at least 1?), demand (do I want at least 1?), desire (check against a desire_threshold), and thirst are met. If not, move to next item.
   2. Add the maximum possible amount of this item to my total order, as limited by demand, thirst, and budget and discount available budget and thirst
4. If I have at least one item to order, enter queue. Otherwise, leave the tavern.

I now have an intricate algorithm to test and existential anxiety because I have not tested this monster of a logic yet. Time to change this...

Debugging the order algo

Of course everything did not work out as intended. A few tests and reviews later, the biggest blunders are ironed out and patrons now order different amounts of beer with reasonable price influence:

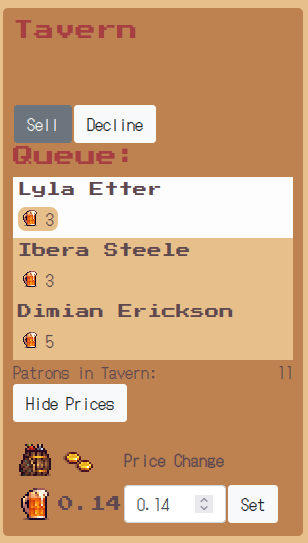
To see how this 'plays' in real application, I need to have the necessary item variety to choose from when ordering. This opens a whole different can of worms for a different day...

Thank you, Desmos!

As the modeling screenshots show, I stumbled upon Desmos while tinkering with the functions. It was a no-hassle and intuitive experience working with their interface. I recommend considering them when playing with plots!