A Random Look at the Engine
This devlog follows the development of one part of Gnomebrew's engine, namely the content generation module.
Fair Warning
Software development is a technical subject. To follow along entirely, some math is required.
Core Module Design
Starting from intent, I outline the most general form of the problem the new module will solve.
I need to generate large amounts of content for Gnomebrew:
- People (Patrons, Adventurers, Bandits, ...)
- (Quest) Items (Weapons, Gems, Beer Ingredients, ...)
- Structures (City, Castle, Cave, ...)
- etc.
This allows me to provide a large player base with varried content.
This challenge is incredibly broad. Being a one-man-show, the content generation module requires a high degree of scalability (to generate great amounts of content) and flexibility (to generate many different types of content).
Content generation is a classic game topic, so I can see what others did before me: Games like Minecraft generate virtually infinite worlds using mechanics of random number generators. By setting the seed, the virtually infinite world is completely defined (and 'just' needs to be generated still). These seeds are a big deal. There are several places on the internet dedicated to exploring/propagating world seeds that create interesting structures.
This level of compression is perfect for Gnomebrew: with just one variable
seeda gigantic amount of content is fully defined, it just hasn't been generated yet.
I will also need source data (e.g. lists of names) as a base for generated content. With this, I can describe the rough outline how generators will work:
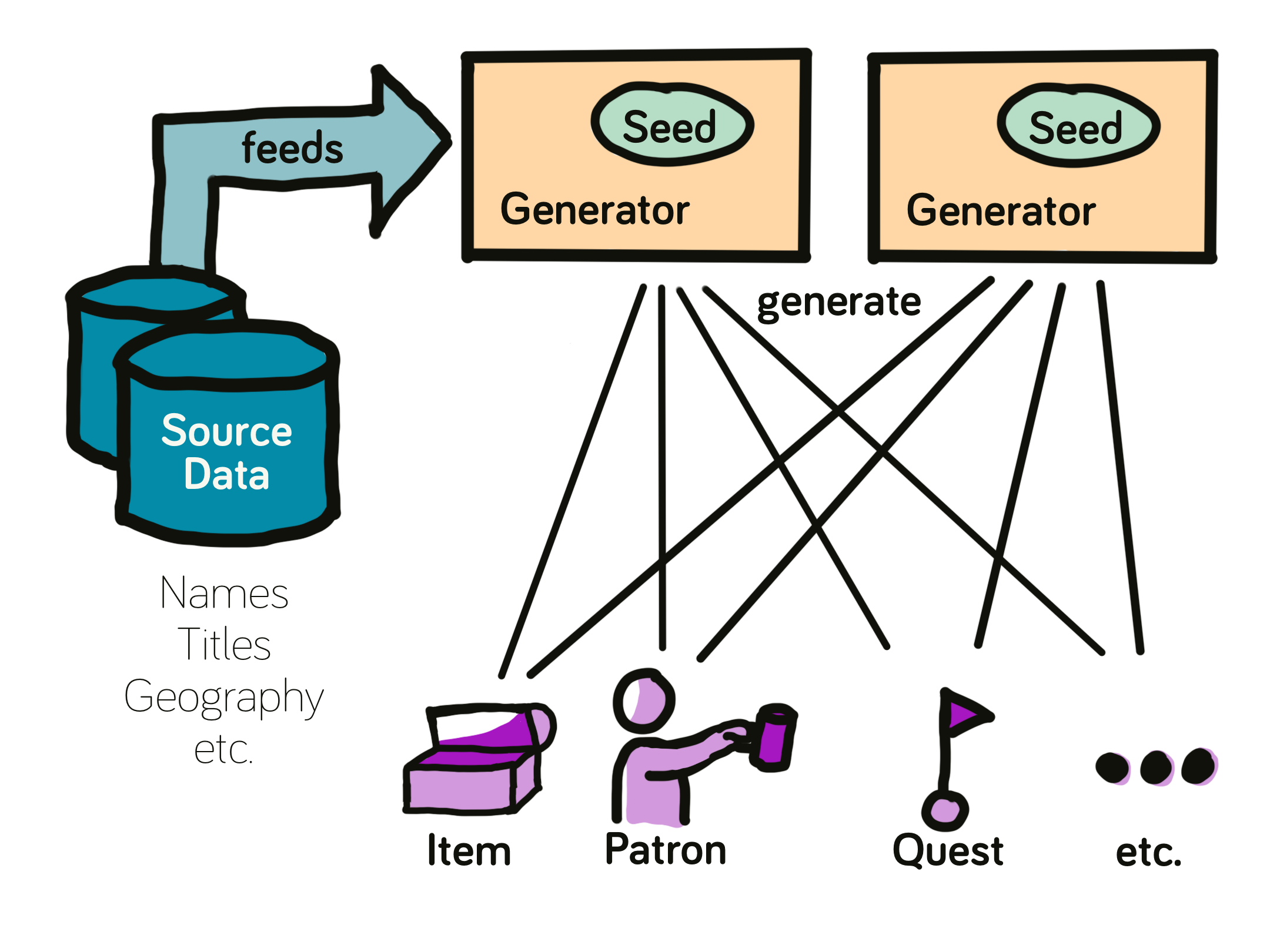
Or, in words: A generator object is created with a seed. It has access to source data like name lists and uses it to generate game objects ready for use.
Two generators with the same seed (and no other difference) will create the same results and different results on different seeds.
Basics of Random Number Generation
The development journey of this module starts with some math: To randomly generate good content, I need a few different ways to do "random" in Gnomebrew.
Fundamental Formula
Luckily, this topic is popular online, so research is a relative breeze. Looking at some sources on RNG I learn that the Linear Congruential Generator is a popular and seductively simple algorithm to generate pseudo-randomness. I decide to start with this algorithm (especially since alternatives are somewhat more involving to code).
In it's most reduced form, this formula creates a series of random numbers:
def next_x(last_x, a, c, m):
return (a * last_x + c) % m
xis the generated random variable and it's initialized with theseed.
a,c, andmare constants that I must define.
Defining the constants
The Wikipedia article linked an enlightening paper on quality inputs for a. In the paper's errata I can find empirically tested values for all constants. The original article contains further background on optimizing computation as well, but for now I will shoot for a simple implementation. I will pick:
-
m = 2 ^ 32This means the generator creates numbers from
0to2 ^ 32. This means, there are4.294.967.296, over 4 billion, options per cycle. More than I need for sure. Since this is a power of 2, it will be very convenient to calculate with. -
a = 29.943.829This is the smallest suggested value for
awith thism. -
c = 182.903The only requirement given by the authors is that c is odd. Additionally, I chose c to not share prime factors with
a.
Since my chosen m is a power of 2, I can 'skip' the actual modulo operation and instead use a bitwise operation to accelerate the calculation. A helpful StackOverflow thread provides a great overview and examples:
To calculate modulo of a power of 2, all I need to do is perform one bitwise AND operation:
z mod 2^32 = z & (2^32-1)
Alltogether, this creates a very lean base code for my Generator:
class Generator:
a = 29943829 # Thank you: https://www.iro.umontreal.ca/~lecuyer/myftp/papers/latrules99Errata.pdf
c = 182903 # Any odd number should work
m = 4294967296 # 2 ^ 32
m_bit_and = m-1 # Value used for bitwise AND to speed up modulo operations
def __init__(self, seed: int):
assert 0 <= seed < Generator.m
self.x = seed
def next(self):
self.x = (Generator.a * self.x + Generator.c) & Generator.m_bit_and
return self.x
def next_limited(self, max_excl: int):
"""
Generates the next number, ensuring it is anywhere between `0` (inclusive) and `max_excl` (exclusive).
:param max_excl: The upper limit of the next number needed (exclusive)
:return: A generated number n with 0 <= n < `max_excl`
"""
return self.next() % max_excl
I'm testing the generator by tallying outputs (for different seeds and output intervals) and am pleased with the results; not that there was much room for surprise following this closely to published work. For a test run tallying a few million results from 12 options, the outcome looks like this:
0: 8.353%
1: 8.316%
2: 8.329%
3: 8.277%
4: 8.336%
5: 8.342%
6: 8.336%
7: 8.365%
8: 8.311%
9: 8.341%
10: 8.335%
11: 8.358%
Looks uniform enough.
Extending the module
Generating Floating Point Numbers
The basic number generation creates integers between 0 and 2^32. I can can easily project this on the unit interval [0;1) to generate a float:
def rand_unit(self) -> float:
"""
Generates a random number between 0 and 1.
:return: A number in [0;1)
"""
return self.next() / Generator.m
I can now stretch the unit interval to whatever interval is required:
def rand_float(self, min_value: float, max_value: float):
return self.rand_unit() * (max_value - min_value) + min_value
Normal Distribution
So far all outcomes have been equally likely, i.e. uniformly distributed.
Reality rarely gives out everything equally: Most things like first names or a person's height will follow different patterns. I want some of these available in my
Generator.
The Normal Distribution is analogous to the famous bell curves many traits fall into. Its normal name hints at how common it is. Definitely worth including.
For this, I'm using the Box-Muller Transform. I can take two uniformly distributed variables and turn them into two normally distributed variables:
def rand_normal(self, **kwargs) -> float:
u_1, u_2 = self.rand_unit(), self.rand_unit()
res = math.sqrt(-2 * math.log(u_1)) * math.cos(2 * math.pi * u_2)
# Deviation now = 1
if 'deviation' in kwargs:
res *= kwargs['deviation']
if 'median' in kwargs:
res += kwargs['median']
return res
It is a shame that I only use one of the two hypothetical variables I could generate from u_1 and u_2. However, if I start worrying about performance edge to this degree, I should probably reconsider Python as backend language in the first place.
Pareto Distribution
Compared to the Normal Distribution, this one is a little more exotic in the RNG-world. At the same time, it's one of the most fascinating ones:
The Pareto Distribution is quite interesting, as it can be found in economics, in sociology, finance, and a lot more fields. More prominently it is known as the 80-20 rule with some examples:
- 20% of all effort yields 80% of all results.
- 20% of all words are used to create 80% of all sentences.
- 20% of all names are used to name 80% of the population.
- 20% of all dungeons contain 80% of all loot.
If you are curious, Michael from VSauce has an excellent video on Zipf's law which is closely related to Pareto.
I want pareto-distributed variables and their 'realism' available for Gnomebrew. This will require some math, but nothing to be afraid of:
Each of the pareto-options (1, 2, 3, etc. to an arbitrary maximum n) has a reciprocal 'weight' that represents how probable the outcome is. By choosing a uniformly random number between 0 and the sum of all weights, I can determine its analogous pareto-element on the number line by finding it's corresponding pareto-option.
Some math background helps recognize the sum of all weights: The total 'weight' of all n options is the n-th Harmonic Number. Thanks to smart mathematicians, I can approximate the n-th Harmonic Number as gamma + ln (n) where gamma is the Euler-Mascheroni Constant.
Some napkin math is needed to find the translation formula:

I now have a very compact function to generate pareto-distributed variables, only requiring one uniform variable and an exponentiation:
def generate_pareto_index(self, num_choices) -> int:
uniform_variable = self.rand_float(0, Generator.euler_mascheroni + math.log(num_choices))
return math.floor(math.exp(uniform_variable-Generator.euler_mascheroni))
Looks great, but when testing this function I get consistenly bad results. The lower options are far off:
Option 0: 18.882% [expected: 32.657%]
Option 1: 22.617% [expected: 16.329%]
Option 2: 13.309% [expected: 10.886%]
Option 3: 9.306% [expected: 8.164%]
Option 4: 7.287% [expected: 6.531%]
Option 5: 5.910% [expected: 5.443%]
Option 6: 5.051% [expected: 4.665%]
Option 7: 4.365% [expected: 4.082%]
Option 8: 3.834% [expected: 3.629%]
Option 9: 3.467% [expected: 3.266%]
Option 10: 3.164% [expected: 2.969%]
Option 11: 2.806% [expected: 2.721%]
This really shows the limitations of the approximating function gamma + ln (n) which is far off for small values of n. Testing the difference between approximation and full calculation confirms the issue:
--- n=1 ---
Harmonic Number: 1.0
With Formula: 0.5772156649015329
Difference: 0.42278433509846713
--- n=2 ---
Harmonic Number: 1.5
With Formula: 1.2703628454614782
Difference: 0.22963715453852185
--- n=3 ---
Harmonic Number: 1.8333333333333333
With Formula: 1.6758279535696428
Difference: 0.1575053797636905
--- n=4 ---
Harmonic Number: 2.083333333333333
With Formula: 1.9635100260214235
Difference: 0.11982330731190949
[...]
--- n=96 ---
Harmonic Number: 5.146763147555442
With Formula: 5.141563856369369
Difference: 0.005199291186072763
--- n=97 ---
Harmonic Number: 5.157072425905957
With Formula: 5.151926643404916
Difference: 0.005145782501041474
--- n=98 ---
Harmonic Number: 5.1672765075386105
With Formula: 5.162183143572105
Difference: 0.005093363966505393
--- n=99 ---
Harmonic Number: 5.177377517639621
With Formula: 5.1723355150361225
Difference: 0.005042002603498297
As expected, the error gets smaller with larger n, so the solution here is simple enough: A lookup dictionary has precomputed values for small Harmonic Numbers prepared:
# Calculate the first harmonic numbers 'by hand', because the approximating function is really bad
# for small values.
MAX_LOOKUP_HARMONIC_NUMBER = 30
# Harmonic Numbers Table
H = {n: sum(1 / i for i in range(1, n + 1)) for n in range(1, MAX_LOOKUP_HARMONIC_NUMBER + 1)}
Now I have the necessary lookup data ready to improve the results for low numbers:
def generate_pareto_index(self, num_choices) -> int:
"""
Generates a pareto index.
Assuming a choice of `num_choices` different options with pareto-distributed probability (first option most
probable, last option least probable).
:param num_choices: The total number of choices.
:return: An index between `0` and `num_choices-1` (each inclusive) that represents the generated
pareto-choice.
"""
if num_choices <= Generator.MAX_LOOKUP_HARMONIC_NUMBER:
# Too small to approximate with function
total_weight = Generator.H[num_choices]
else:
# Big enough to use approximate with function
total_weight = Generator.euler_mascheroni + math.log(num_choices)
# Generate a uniformly distributed random value in the weight-space defined
uniform_variable = self.rand_float(0, total_weight)
if uniform_variable >= max(Generator.H.values()):
# Variable is greater than the largest value in the lookup. Use approximation
return math.floor(math.exp(uniform_variable - Generator.euler_mascheroni)) # floor to be zero indexed
else:
# Variable within value range of lookup table. Use it.
return min(filter(lambda n: uniform_variable < Generator.H[n],
Generator.H.keys())) - 1 # -1 to be zero indexed
Research: Data Sourcing
Sourcing data is less of a programming and more of a research task. The mission is clear:
Collect as many useful buckets of data that can be used during generation as possible.
Simple Data: CSV Files
A dedicated data directory stores CSV files. Everything in here is accessible in engine for generation purposes and beyond. Right now, this is Gnomebrew's data directory stores around 1.6MB of data and looks like this:
data
├── adjectives
│ ├── adjectives.csv
│ └── traits.csv
├── names
│ ├── dwarf_female_names_syl1.csv
│ ├── dwarf_female_names_syl2.csv
│ ├── dwarf_female_names_syl3.csv
│ ├── dwarf_male_names_syl1.csv
│ ├── dwarf_male_names_syl2.csv
│ ├── dwarf_male_names_syl3.csv
│ ├── dwarf_surnames_syl1.csv
│ ├── dwarf_surnames_syl2.csv
│ ├── elf_female_names.csv
│ ├── elf_male_names.csv
│ ├── elf_nonbinary_names.csv
│ ├── elf_surnames_syl1.csv
│ ├── elf_surnames_syl2.csv
│ ├── half-elf_female_names_syl1.csv
│ ├── half-elf_female_names_syl2.csv
│ ├── half-elf_male_names_syl1.csv
│ ├── half-elf_male_names_syl2.csv
│ ├── half-elf_surnames_syl1.csv
│ ├── half-elf_surnames_syl2.csv
│ ├── human_female_names.csv
│ ├── human_male_names.csv
│ ├── human_nonbinary_names.csv
│ ├── human_surnames.csv
│ ├── orc_female_names.csv
│ ├── orc_male_names.csv
│ └── titles.csv
├── nouns
│ └── nouns.csv
└── sources.md
The sources.md file tracks where I fetched data from. The largest data sources as of now sources are Princeton's WordNet and - in one lucky case - source files from a data-driven article on a related problem.
A few tools allow me to streamline the process of compiling and cleaning the data files ready for production, most notably the excellent Pandas module. The popular module essentially provides "Excel for Python" which makes editing the data in a console easy and efficient.
Dealing with complicated data: Generation Rules
In development I realized that I needed a higher degree of flexibility than the CSV-based data directory provided. Since Gnomebrew is used to complexity, that's no problem: One new JSON object type is all that I needed to encode research data efficiently for Gnomebrew's generation.
The new generation_rules collection in the game's MongoDB instance manages these objects. Their exact makeup would break this post's scope, but at their core they allow for more configuration options thanks to JSON's flexibility. For example: This data would be associated with generating Ocean regions:
{
"game_id": "gen.region.ocean",
"name": "Ocean",
"description": "Deep water as far as the eye can see. Don't approach unless you can swim.",
"gen_attr": {
"Region Name": {
"str": "<Context Adjective> Ocean|<Context Adjective> Sea|<Context Name>'s Seas"
}
},
"env_rules": {
"Prevalent Structures": {
"City": -3,
"Island": 50,
"Water": 900,
"River": -100,
"Coral Reef": 50,
"Cliffs": 30,
"Castle": -10
},
"Prevalent People": {
"triton": 30
},
"Context Nouns": [
"Depth"
],
"Context Adjectives": [
"Vast",
"Deep",
"Blue",
"Rising"
],
"Temperature": 0,
"Temperature Fluctuation": 1,
"Population Density": -10
}
}
These objects allow me to access all kinds of contextual data during the actual generation process. I can use this to provide some simulated bells and whistles in gameplay like:
- adjust a modeled temperature across a game map
- change up the composition of patrons based on tavern location
- name legendary items and locations with contextually fitting names
Software Architecture: The Generator
To ensure my Generator class can keep up with arbitrary complexity, I base its' architecture on a simple type system. Each generation type describes a class of things that can be generated, e.g. "Patron", "Item", "Quest Item", "First Name", "Gender" etc. Each of these type classes will come with its' own generation function.
How this works in practice is easy to follow.
A Simple Generation Example: Personality
In a previous devlog I have outlined how personality in game is made of (independently and) randomly assigned Big Five parameters. Integrating this into the Generator is adding a decorated function:
@Generator.generation_type(gen_type='Personality', ret_type=dict)
def generate_personality(gen: Generator):
personality = dict()
personality['extraversion'] = gen.rand_normal(min=-1, max=1)
personality['agreeableness'] = gen.rand_normal(min=-1, max=1)
personality['openness'] = gen.rand_normal(min=-1, max=1)
personality['conscientiousness'] = gen.rand_normal(min=-1, max=1)
personality['neuroticism'] = gen.rand_normal(min=-1, max=1)
return personality
The function's variable gen provides the (appropriately seeded and set up) Generator that is used for the generation alongside with its quick access to data; more advanced processes would actually make use of it, but since personality is entirely random, no data is needed here.
Generating Complex Things: People
The actual code for a complex Person is remarkably clean, cascading down the generation tasks from Person to its simpler generation tasks:
@Generator.generation_type(gen_type='Person', ret_type=Person)
def generate_person(gen: Generator):
"""
Generates a person.
:param gen: The generator to use.
:return: The generated Person.
"""
data = dict()
data['game_id'] = f"entity.{generate_uuid()}" # By convention: every generated entity has a `entity` uuid Game ID
data['entity_class'] = 'person'
data['race'] = gen.generate('Race')
data['age'] = gen.generate('Person Age')
data['gender'] = gen.generate('Gender')
data['background'] = gen.generate('Background')
data['looks'] = gen.generate('Person Looks')
data['name'] = gen.generate('Person Name')
# Maybe the person will have a title. That's up to the character's background
bg: Background = Background.from_id(f"background.{data['background']}")
if bg.generate_has_title(gen):
data['title'] = bg.generate_title(gen)
data['personality'] = gen.generate('Personality')
data['size'] = gen.generate('Person Size')
return Person(data)
This clean code really illustrates the value of this architecture approach: Every aspect can be outsourced to its own generatable type, keeping the code modular and easy to follow.
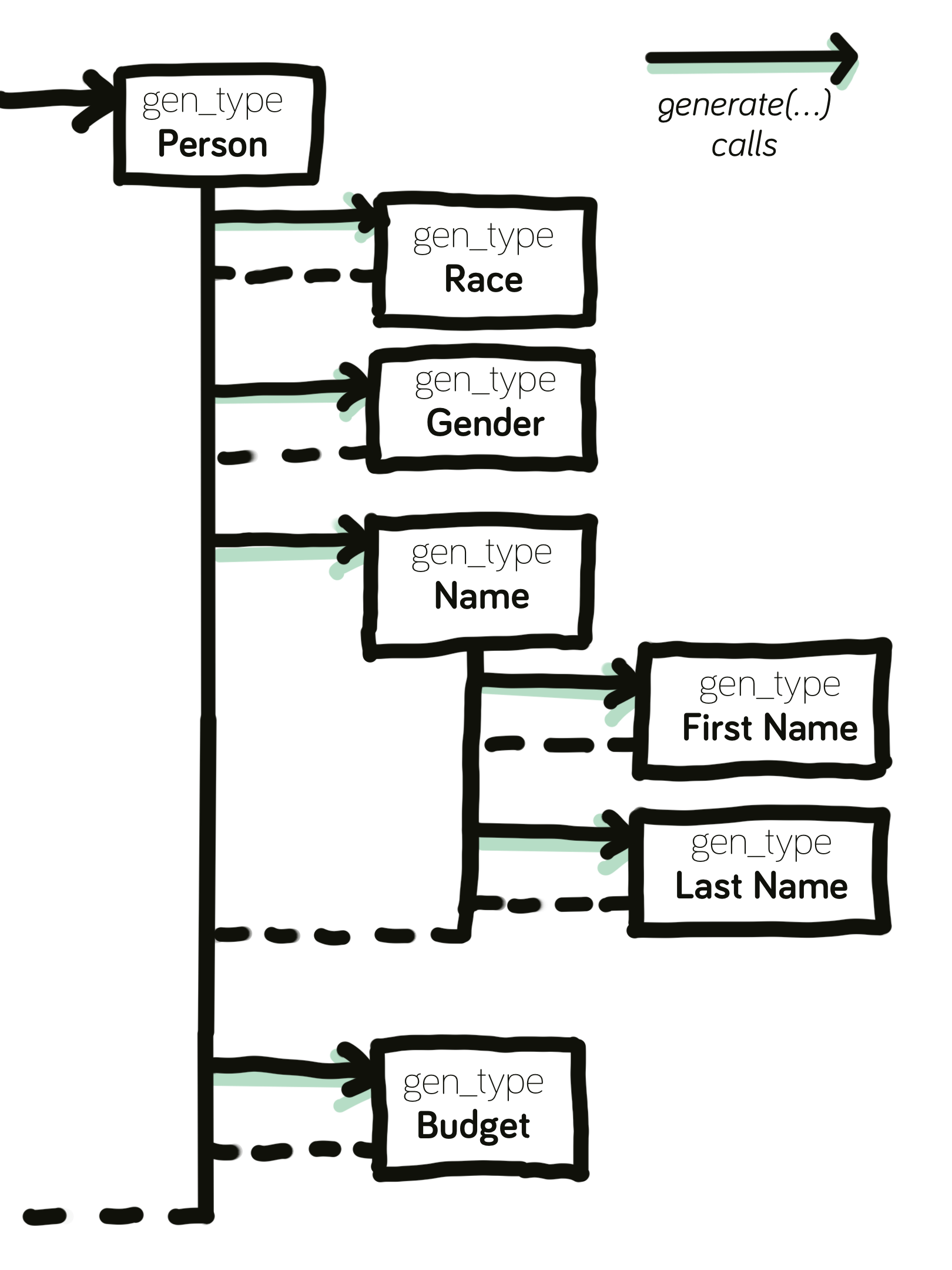
Person type generation. Every aspect of the person is outsourced into its own gen_type.A Generator Memory
This control flow looks nice, but glosses over a core challenge I didn't address yet. In the code examples so far, the generator only needed to pick completely at random or delegate. For example, all parameters of Personality are random and independent values (between -1 and 1). This is not the case for most elements:
Consider a generated
Person. The person'sFirst NameandGenderare generated in separate functions. However, the output for the first name highly depends on a previously generated variable: I use as many different name sets for different genders/races as possible.The
Generatorneeds some form of memory to keep track of what was generated before that works smartly within this context:
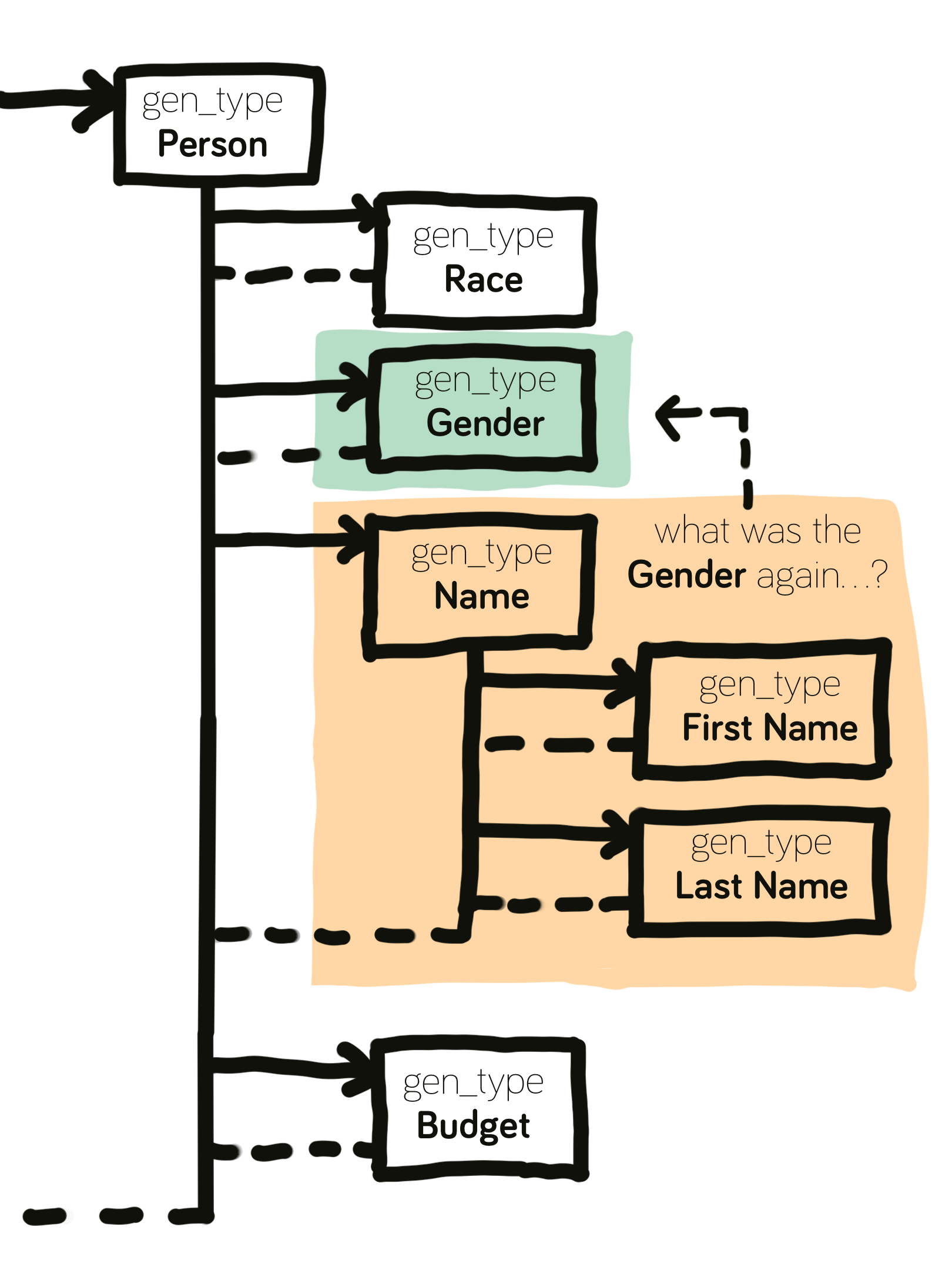
Every gen_type is executed in an insular function with no access to each other's data. After the Gender has been generated, the next gen_type called, Name, would need to know which type of name list to pick based on Gender (and technically also Race).
The call to generate the Name has no way (yet) of knowing happened during the previous generation. Time to fix this.
Implementing Generator Memory
An elegant way to resolve this problem is using the generate function as a stack counter and disvalidating results when their lifetime in the stack is over:
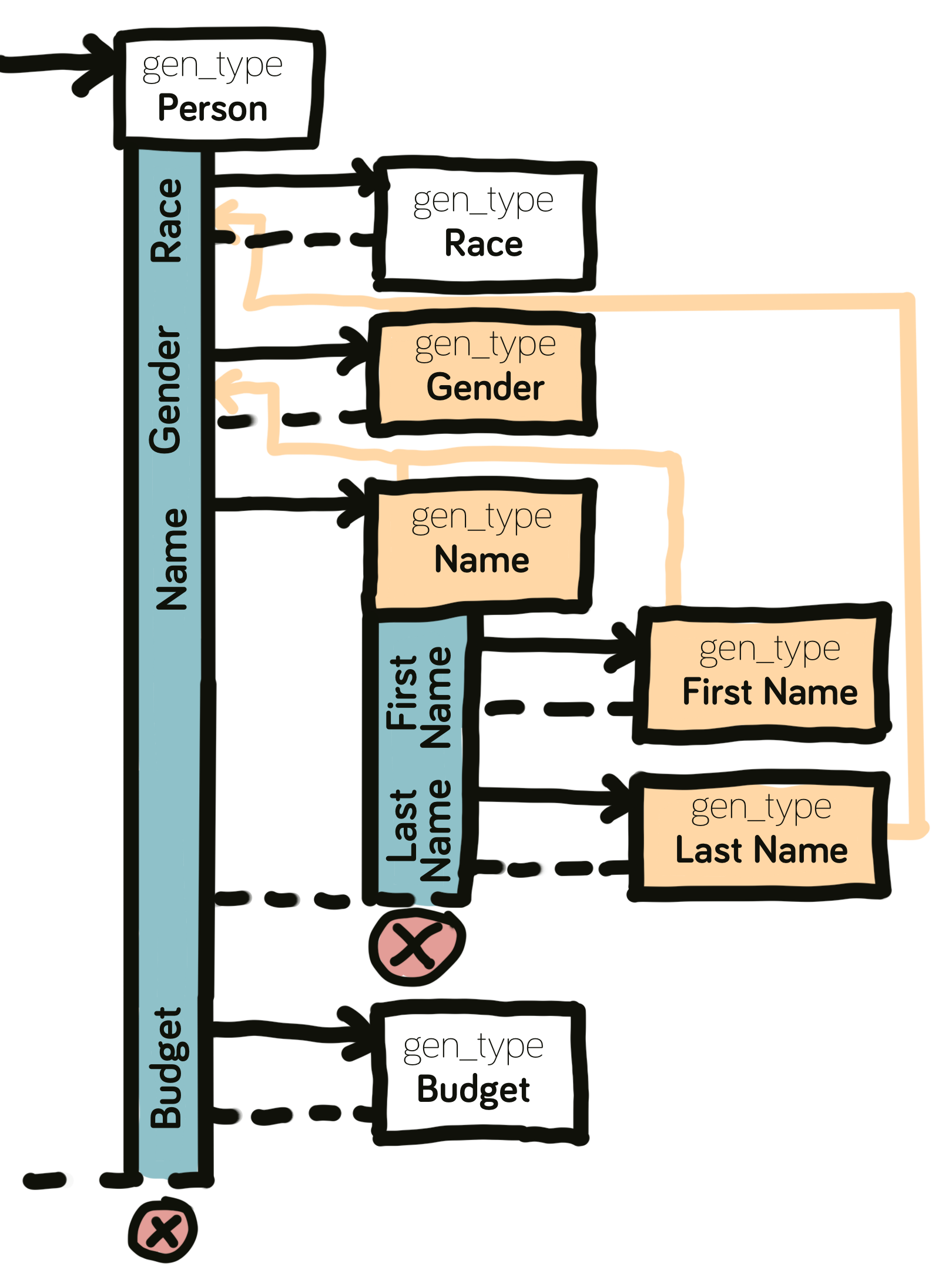
In words: The Generator's memory tracks all results automatically. This way, it can be used during runtime to check for previous generation results.
The Generator keeps track of its memory and automatically clears memory once the corresponding gen_type call finished. This makes it possible to generate multiple objects (e.g. a swarm of patrons ready to enter the tavern) with no memory overlap.
I'm implementing the memory features in an outside class Environment. This way I can provide different generators with the same environment to create variations (e.g. to quickly get many "Half-Elf Female Royal Wizard"s).
Now, the generator provides access to its' generation memory with the get_variable function:
@Generator.generation_type(gen_type='First Name', ret_type=str)
def generate_first_name(gen: Generator):
# Chance for multi names
if gen.rand_int_limited(50) > 40:
return f"{gen.generate('First Name')} {gen.generate('First Name')}"
gender = gen.get_variable('Gender', default=None)
race = gen.get_variable('Race', default=None)
if gender is None:
# No gender was defined. Choose at random
gender = gen.choose(Person.GENDER_CHOICES)
if race is None:
# No race was defined. Choose at random
race = gen.choose(Person.RACE_BASE_CHOICES)
# Access the data directory based on Gender & Race (e.g. female elf) and pick
return race.generate_name(gen, gender, 'names')
The Generation Journey
With all of this implemented, I have a Generator that will have no issues adapting to Gnomebrew's ever changing scope.
Looking back we had a this was a fun and long day at the workshop: